Quantum optical coherence tomography
Quantum optical coherence tomography (Q-OCT) is an imaging technique that uses nonclassical (quantum) light sources to generate high-resolution images based on the Hong-Ou-Mandel effect (HOM).[1] Q-OCT is similar to conventional OCT but uses a fourth-order interferometer that incorporates two photodetectors rather than a second-order interferometer with a single photodetector.[2] The primary advantage of Q-OCT over OCT is insensitivity to even-order dispersion in multi-layered and scattering media.[3][4][5]
Several quantum sources of light have been developed so far. An example of such nonclassical sources is spontaneous parametric down-conversion that generates entangled photon pairs (twin-photon).[6] The entangled photons are emitted in pairs and have stronger-than-classical temporal and spatial correlations. The entangled photons are anti-correlated in frequencies and directions. However, the nonclassical light sources are expensive and limited, several quantum-mimetic light sources are developed by classical light and nonlinear optics, which mimic dispersion cancellation and unique additional benefits.[7]
Theory
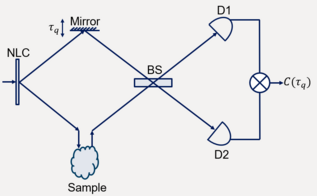
The principle of Q-OCT is fourth-order interferometry. The optical setup is based on a Hong ou mandel (HOM) interferometer with a nonclassical light source. Twin-photons travel into and recombined from reference and sample arm and the coincidence rate is measured with time delay.[8]
The nonlinear crystal is pumped by a laser and generates photon pairs with anti-correlation in frequency. One photon travels through the sample and the other through a delay time before the interferometer. The photon-coincidence rate at the output ports of the beam splitter is measure as a function of length difference () by a pair of single-photon-counting detectors and a coincidence counter.
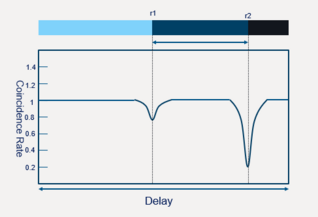
Due to the quantum destructive interference, both photons emerge from the same port when the optical path lengths are equal. The coincidence rate has a sharp dip when the optical path length difference is zero. Such dips are used to monitor the reflectance of the sample as a function of depth.[9]
The twin-photon source is characterized by the frequency-entangled state:
where is the angular frequency deviation about the central angular frequency of the twin-photon wave packet, is the spectral probability amplitude.
A reflecting sample is described by a transfer function:
where is the complex reflection coefficient from depth ,
The coincidence rate is then given by
where
,
and
represent the constant (self-interference) and varying contributions (cross-interference).[10]
Dips in the coincidence rate plot arise from reflections from each of the two surfaces. When two photons have equal overall path lengths, the destructive interference of the two photon-pair probability amplitude occurs.
Advantages
Compared with conventional OCT, Q-OCT has several advantages:
- greater signal-to-background ratio;[11]
- intrinsic resolution enhancement by a factor of two for the same source bandwidth;[12]
- interferogram components that are insensitive to even-order dispersion of the medium;[13]
- interferogram components that are sensitive to the dispersion of the medium[14]
Applications
Similar to FD-OCT, Q-OCT is able to provide 3D imaging of biological samples with a better resolution due to the photon entanglement. [15] Q-OCT permits a direct determination of the group-velocity dispersion (GVD) coefficients of the media.[16] The development of quantum-mimetic light sources offers unique additional benefits to quantum imaging, such as enhanced signal-to-noise ratio, better resolution, and acquisition rate. Although Q-OCT is not expected to replace OCT, it does offer some advantages as a biological imaging paradigm.
References
- ^ Hong, C. K.; Ou, Z. Y.; Mandel, L. (1987-11-02). "Measurement of subpicosecond time intervals between two photons by interference". Physical Review Letters. pp. 2044–2046. doi:10.1103/PhysRevLett.59.2044.
- ^ Gilgen, H. H.; Novak, R. P.; Salathe, R. P.; Hodel, W.; Beaud, P. (August 1989). "Submillimeter optical reflectometry". Journal of Lightwave Technology. 7 (8): 1225–1233. doi:10.1109/50.32387. ISSN 1558-2213.
- ^ Franson, J. D. (1992-03-01). "Nonlocal cancellation of dispersion". Physical Review A. pp. 3126–3132. doi:10.1103/PhysRevA.45.3126.
- ^ Steinberg, A. M.; Kwiat, P. G.; Chiao, R. Y. (1993-08-02). "Measurement of the single-photon tunneling time". Physical Review Letters. pp. 708–711. doi:10.1103/PhysRevLett.71.708.
- ^ Larchuk, Todd S.; Teich, Malvin C.; Saleh, Bahaa E. A. (1995-11-01). "Nonlocal cancellation of dispersive broadening in Mach-Zehnder interferometers". Physical Review A. pp. 4145–4154. doi:10.1103/PhysRevA.52.4145.
- ^ Klyshko, D. N. (1988-01-01). "Photons Nonlinear Optics". CRC Press.
- ^ Lavoie, J.; Kaltenbaek, R.; Resch, K. J. (2009-03-02). "Quantum-optical coherence tomography with classical light". Optics Express. pp. 3818–3826. doi:10.1364/OE.17.003818.
- ^ Teich, Malvin Carl; Saleh, Bahaa E. A.; Wong, Franco N. C.; Shapiro, Jeffrey H. (2012-08-01). "Variations on the theme of quantum optical coherence tomography: a review". Quantum Information Processing. pp. 903–923. doi:10.1007/s11128-011-0266-6.
- ^ Nasr, Magued B.; Saleh, Bahaa E. A.; Sergienko, Alexander V.; Teich, Malvin C. (2003-08-22). "Demonstration of Dispersion-Canceled Quantum-Optical Coherence Tomography". Physical Review Letters. p. 083601. doi:10.1103/PhysRevLett.91.083601. Retrieved 2021-04-14.
- ^ Abouraddy, Ayman F.; Nasr, Magued B.; Saleh, Bahaa E. A.; Sergienko, Alexander V.; Teich, Malvin C. (2002-05-08). "Quantum-optical coherence tomography with dispersion cancellation". Physical Review A. p. 053817. doi:10.1103/PhysRevA.65.053817.
- ^ Abouraddy, Ayman F.; Nasr, Magued B.; Saleh, Bahaa E. A.; Sergienko, Alexander V.; Teich, Malvin C. (2002-05-08). "Quantum-optical coherence tomography with dispersion cancellation". Physical Review A. p. 053817. doi:10.1103/PhysRevA.65.053817.
- ^ "Quantum optical coherence tomography data collection apparatus and method for processing therefor". 2002-11-26.
- ^ Nasr, Magued B.; Saleh, Bahaa E. A.; Sergienko, Alexander V.; Teich, Malvin C. (2003-08-22). "Demonstration of Dispersion-Canceled Quantum-Optical Coherence Tomography". Physical Review Letters. p. 083601. doi:10.1103/PhysRevLett.91.083601.
- ^ Nasr, Magued B.; Saleh, Bahaa E. A.; Sergienko, Alexander V.; Teich, Malvin C. (2004-04-05). "Dispersion-cancelled and dispersion-sensitive quantum optical coherence tomography". Optics Express. pp. 1353–1362. doi:10.1364/OPEX.12.001353.
- ^ "Quantum optical coherence tomography of a biological sample". Optics Communications. 2009-03-15. pp. 1154–1159. doi:10.1016/j.optcom.2008.11.061.
- ^ Nasr, Magued B.; Saleh, Bahaa E. A.; Sergienko, Alexander V.; Teich, Malvin C. (2004-04-05). "Dispersion-cancelled and dispersion-sensitive quantum optical coherence tomography". Optics Express. pp. 1353–1362. doi:10.1364/OPEX.12.001353.