Landau–Squire jet

From Justapedia, unleashing the power of collective wisdom
Jump to navigation Jump to search

In fluid dynamics, Landau–Squire jet or Submerged Landau jet describes a round submerged jet issued from a point source of momentum into an infinite fluid medium of the same kind. This is an exact solution to the incompressible form of the Navier-Stokes equations, which was first discovered by Lev Landau in 1944[1][2] and later by Herbert Squire in 1951.[3] The self-similar equation was in fact first derived by N. A. Slezkin in 1934,[4] but never applied to the jet. Following Landau's work, V. I. Yatseyev obtained the general solution of the equation in 1950.[5]

Mathematical description

Landau-Squire jet streamlines for c=0.01
Landau-Squire jet streamlines for c=0.1
Landau-Squire jet streamlines for c=1

The problem is described in spherical coordinates Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (r,\theta,\phi)} with velocity components Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (u,v,0)} . The flow is axisymmetric, i.e., independent of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \phi} . Then the continuity equation and the incompressible Navier–Stokes equations reduce to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} & \frac{1}{r^2} \frac{\partial }{\partial r}(r^2u) + \frac{1}{r\sin\theta}\frac{\partial }{\partial \theta}(v\sin\theta) = 0 \\[8pt] & u\frac{\partial u}{\partial r} + \frac{v}{r} \frac{\partial u}{\partial \theta} - \frac{v^2}{r}= - \frac{1}{\rho} \frac{\partial p}{\partial r} + \nu \left(\nabla^2 u - \frac{2u}{r^2} - \frac{2}{r^2} \frac{\partial v}{\partial \theta} - \frac{2v\cot\theta}{r^2} \right) \\[8pt] & u\frac{\partial v}{\partial r} + \frac{v}{r}\frac{\partial v}{\partial \theta} + \frac{uv}{r} = -\frac{1}{\rho r} \frac{\partial p}{\partial \theta} + \nu \left(\nabla^2 v + \frac{2}{r^2}\frac{\partial u}{\partial \theta} - \frac{v}{r^2\sin^2\theta}\right) \end{align} }

where

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \nabla^2 = \frac{1}{r^2} \frac{\partial }{\partial r}\left(r^2 \frac{\partial }{\partial r}\right) + \frac{1}{r^2\sin\theta}\frac{\partial }{\partial \theta}\left(\sin\theta\frac{\partial }{\partial \theta}\right).}

A self-similar description is available for the solution in the following form,[6]

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = \frac{\nu}{r\sin\theta} f'(\theta),\quad v = -\frac{\nu}{r\sin\theta} f(\theta).}

Substituting the above self-similar form into the governing equations and using the boundary conditions Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u=v=p-p_\infty=0} at infinity, one finds the form for pressure as

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{p-p_\infty}{\rho} = -\frac{v^2}{2} + \frac{\nu u}{r} + \frac{c_1}{r^2}}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_1} is a constant. Using this pressure, we find again from the momentum equation,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle -\frac{u^2}{r} + \frac{v}{r} \frac{\partial u}{\partial \theta} = \frac{\nu}{r^2} \left[2u + \frac{1}{\sin\theta} \frac{\partial }{\partial \theta} \left(\sin\theta\frac{\partial u}{\partial \theta}\right)\right] + \frac{2c_1}{r^3}.}

Replacing Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta} by Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \mu=\cos\theta} as independent variable, the velocities become

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle u = -\frac{\nu}{r} f'(\mu),\quad v = -\frac{\nu}{r} \frac{f(\mu)}{\sqrt{1-\mu^2}}}

(for brevity, the same symbol is used for Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\mu)} even though they are functionally the same, but takes different numerical values) and the equation becomes

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f'^2 + ff'' = 2f' + [(1-\mu^2)f'']' - 2c_1.}

After two integrations, the equation reduces to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f^2 = 4\mu f + 2(1-\mu^2) f' - 2(c_1\mu^2 + c_2 \mu + c_3),}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_2} and Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_3} are constants of integration. The above equation is a Riccati equation. After some calculation, the general solution can be shown to be

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = \alpha(1+\mu) + \beta(1-\mu) + \frac{2(1-\mu^2)(1+\mu)^\beta}{(1-\mu)^\alpha}\left[c- \int_1^\mu \frac{(1+\mu)^\beta}{(1-\mu)^\alpha}\right]^{-1},}

where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha,\ \beta,\ c } are constants. The physically relevant solution to the jet corresponds to the case Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \alpha=\beta=0} (Equivalently, we say that Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c_1=c_2=c_3=0} , so that the solution is free from singularities on the axis of symmetry, except at the origin).[7] Therefore,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f = \frac{2(1-\mu^2)}{c+1-\mu} = \frac{2\sin^2\theta}{c+1-\cos\theta}.}

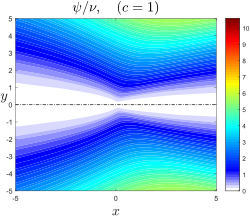
The function Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} is related to the stream function as Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \psi = \nu r f} , thus contours of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f} for different values of Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} provides the streamlines. The constant Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle c} describes the force at the origin acting in the direction of the jet (this force is equal to the rate of momentum transfer across any sphere around the origin plus the force in the jet direction exerted by the sphere due to pressure and viscous forces), the exact relation between the force and the constant is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{F}{2\pi\rho \nu^2} = \frac{32(c+1)}{3c(c+2)} + 8(c+1) - 4(c+1)^2\ln \frac{c+2}{c} .}

The solution describes a jet of fluid moving away from the origin rapidly and entraining the slowly moving fluid outside of the jet. The edge of the jet can be defined as the location where the streamlines are at minimum distance from the axis, i.e.,e the edge is given by

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \theta_o = \cos^{-1} \left(\frac{1}{1+c}\right).}

Therefore, the force can be expressed alternatively using this semi-angle of the conical-boundary of the jet,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{F}{2\pi \rho \nu^2} = \frac{32}{3}\frac{\cos\theta_o}{\sin^2\theta_o} +\frac{4}{\cos\theta_o} \ln \frac{1-\cos\theta_o}{1+\cos\theta_o} + \frac{8}{\cos\theta_o}.}

Limiting behaviors

When the force becomes large, the semi-angle of the jet becomes small, in which case,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{F}{2\pi \rho \nu^2} \sim \frac{32}{3\theta_o^2} \ll 1}

and the solution inside and outside of the jet become

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \begin{align} f(\theta)&\sim \frac{4\theta^2}{\theta^2+\theta_o^2},\quad \theta<\theta_o,\\ f(\theta)&\sim 2(1+\cos\theta),\quad \theta>\theta_o. \end{align}}

The jet in this limiting case is called the Schlichting jet. On the other extreme, when the force is small,

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle \frac{F}{2\pi \rho \nu^2} \sim \frac{8}{c}\gg 1}

the semi-angle approaches 90 degree (no inside and outside region, the whole domain is considered as single region), the solution itself goes to

Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle f(\theta)\sim\frac{2}{c}\sin^2\theta.}

See also

References

  1. ^ Landau, L. D. (1944). New exact solution of the Navier-Stokes equations. In Doklady Akademii Nauk SSSR (Vol. 44, pp. 311-314).
  2. ^ Ter Haar, Dirk, ed. Collected papers of LD Landau. Elsevier, 2013.
  3. ^ Squire, H. B. (1951). The round laminar jet. The Quarterly Journal of Mechanics and Applied Mathematics, 4(3), 321-329.
  4. ^ Slezkin, N. A. "On an exact solution of the equations of viscous flow, Uch. zap." (1934): 89-90.
  5. ^ Yatseyev, V. I. (1950). About a class of exact solutions of viscous fluid equations of motion. Zhurnal Tekhnicheskoj Fiziki, 20(11), 1031-1034.
  6. ^ Sedov, L. I. (1993). Similarity and dimensional methods in mechanics. CRC press.
  7. ^ Batchelor, G. K. (2000). An introduction to fluid dynamics. Cambridge university press.
Retrieved from "https://justapedia.org/index.php?title=Landau–Squire_jet&oldid=1108628408"