Convex curve

A convex curve (black) forms a connected subset of the boundary of a convex set (blue), and has a supporting line (red) through each of its points.

A parabola, a convex curve that is the graph of the convex function

f(x)=x^{2}

In geometry, a convex curve is a plane curve that has a supporting line through each of its points. Examples of convex curves include the boundaries of convex sets and the graphs of convex functions.

Important subclasses of convex curves include the closed convex curves (the boundaries of convex sets), the smooth curves that are convex, and the strictly convex curves, which have the additional property that each supporting line passes through a unique point of the curve. Combinations of these properties have also been considered.

Definitions

A plane curve is the image of any continuous function from an interval to the Euclidean plane. Intuitively, it is a set of points that could be traced out by a moving point. Often, the function used to describe this motion is required not only to be continuous, but also regular, meaning that the moving point never slows to a halt or reverses direction. A plane curve is closed if the two endpoints of the interval are mapped to the same point in the plane, and it is simple if no other two points coincide. There are multiple definitions of smooth curves, involving the derivatives of the function defining the curve. If it is regular and has a derivative everywhere, then each interior point of the curve has a tangent line. If, in addition, the second derivative exists everywhere, then each of these points has a well-defined curvature.^[1]

Among the plane curves, convex curves can be defined in several equivalent ways, including by their supporting lines, by the sets they form boundaries of, and by their intersections with lines.

Supporting lines

A supporting line is a line containing at least one point of the curve, for which the curve is contained in one of the two half-planes bounded by the line. A plane curve is called convex if it has a supporting line through each of its points.^[2] Every convex curve is simple: it cannot cross or intersect itself.

Supporting lines and tangent lines are not the same thing,^[3] but for convex curves, every tangent line is a supporting line.^[2] At a point of a curve where a tangent line exists, there can only be one supporting line, the tangent line.^[4] Therefore, a smooth curve is convex if it lies on one side of each of its tangent lines. This may be used as an equivalent definition of convexity for smooth curves, or more generally for piecewise smooth curves.^[5]^[a]

Boundaries of convex sets

A convex curve may be alternatively defined as a connected subset of the boundary of a convex set in the Euclidean plane.^[2] Not every convex set has a connected boundary,^[b] but when it does, the whole boundary is an example of a convex curve. The boundary of a bounded convex set (one that lies entirely within a sufficiently large circle) forms a closed curve. By the Jordan curve theorem, a simple closed curve divides the plane into interior and exterior regions, and another equivalent definition of a closed convex curve is that it is a simple closed curve whose union with its interior is a convex set.^[8] Unbounded convex sets, such as the epigraphs of convex functions, have boundaries (the graphs of the same functions) that are not closed curves. In either case, when a convex curve forms the boundary of a convex set, it has no endpoints.

This definition is equivalent to the definition of convex curves from support lines. Every convex curve, defined as a curve with a support line through each point, is a subset of the boundary of its own convex hull. Every connected subset of the boundary of a convex set has a support line through each of its points.^[2]

Intersection with lines

For a convex curve, every line in the plane intersects the curve in one of four ways: its intersection can be the empty set, a single point, a pair of points, or an interval. In the cases where a closed curve intersects in a single point or an interval, the line is a supporting line. This can be used as an alternative definition of the convex curves: they are the Jordan curves (connected simple curves) for which every intersection with a line has one of these four types. This definition can be used to generalize convex curves from the Euclidean plane to certain other linear spaces, with the same property that every point belongs to a supporting line.^[9]

Strict convexity

A strictly convex curve is a simple curve in convex position, meaning that none of its points is a convex combination of any other subset of its points. Equivalently, it is a convex curve that does not contain any line segments, a curve that intersects any line in at most two points,^[9] or a connected subset of the boundary of a strictly convex set, one for which every point of the curve is an extreme point of the set.

Strictly convex curves can be defined as the curves that are locally equivalent (under an appropriate coordinate transformation) to the graphs of strictly convex functions.^[10]^[c]

Properties

Length and area

Every closed convex curve (one that is the boundary of a bounded convex set) has a well-defined finite length. These curves are a subset of the rectifiable curves. Their length may be given by a form of the Crofton formula as $\pi$ times the expected value of the length of a projection of the curve onto a randomly-oriented line.^[2]

According to Newton's theorem about ovals, the area cut off from an infinitely differentiable convex curve by a line cannot be an algebraic function of the coefficients of the line.^[11]

A smooth convex curve through 13 integer lattice points

It is not possible for a short strictly convex curve to pass through many points of the integer lattice. If the curve has length $L$ , then according to a theorem of Vojtěch Jarník, the number of lattice points that it can pass through is at most

{\frac {3}{\sqrt[{3}]{2\pi }}}L^{2/3}+O(L^{1/3}),

as expressed in big O notation. The bound cannot be improved as there exist smooth strictly convex curves through this many points.^[12]

Supporting lines and support function

A strictly convex curve can have at most a countable set of singular points, where it has more than one supporting line. All of the remaining points must be non-singular, and the unique supporting line at these points is necessarily a tangent line. This implies that the non-singular points form a dense set in the curve.^[13]

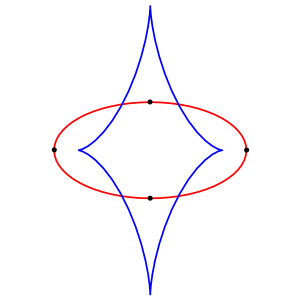
A closed strictly convex closed curve has a continuous support function, mapping each direction of supporting lines to their signed distance from the origin. It is an example of a hedgehog, a type of curve determined as the envelope of a system of lines with a continuous support function. The hedgehogs also include non-convex curves, such as the astroid, and even self-crossing curves, but the smooth strictly convex curves are the only hedgehogs that have no singular points.^[14]

Every curve has at most two supporting lines in each direction. For a bounded curve that does not lie on a single line of the same direction, there are exactly two. Therefore, if a curve has three distinct parallel tangent lines, at least one of them cannot be a supporting line, there can be no other supporting line through the same point, and the curve is not convex. If a smooth closed curve is non-convex, it has a point whose tangent line is not a supporting line, and this line has two parallel supporting lines that are also tangent. Therefore, a smooth closed curve is convex if and only if it does not have three parallel tangent lines.^[5]^[d]

Curvature

An ellipse (red) and its evolute (blue), the locus of its centers of curvature. The four marked vertices of the ellipse correspond to the four cusps of the evolute.

According to the four-vertex theorem, every smooth closed convex curve has at least four vertices, points that are local minima or local maxima of curvature.^[15]

Curvature can be used to characterize the smooth closed curves that are convex.^[5] The curvature depends in a trivial way on the parameterization of the curve: if a regularly parameterization of a curve is reversed, the same set of points results, but its curvature is negated.^[1] A smooth simple closed curve, with a regular parameterization, is convex if and only if its curvature has a consistent sign: always non-negative, or always non-positive. If it is non-convex, it has three parallel tangents, two of them oriented in the same way, and between these two the curve must pass through an inflection point where its curvature changes sign. If its curvature changes sign at an inflection point, then the tangent line there is not a supporting line, and there can be no other supporting line at that point.^[5]^[e]

The total absolute curvature of a smooth convex curve,

\int |\kappa (s)|ds,

is at most

2\pi

. It is exactly

2\pi

for closed convex curves, equalling the total curvature of these curves, and of any simple closed curve. For convex curves, the equality of total absolute curvature and total curvature follows from the fact that the curvature has a consistent sign. For closed curves that are not convex, the total absolute curvature is always greater than

2\pi

, and its excess can be used as a measure of how far from convex the curve is. More generally, by Fenchel's theorem, the total absolute curvature of a closed smooth space curve is at least

2\pi

, with equality only for convex plane curves.^[17]^[18]

Related shapes

An oval with a horizontal axis of symmetry

Smooth closed convex curves with an axis of symmetry, such as an ellipse or Moss's egg, may sometimes be called ovals.^[19] However, in finite projective geometry, ovals are instead defined as sets for which each point has a unique line disjoint from the rest of the set, a property that in Euclidean geometry is true of the smooth strictly convex closed curves.^[9]

The boundary of any convex polygon forms a convex curve (one that is a piecewise linear curve and not strictly convex). A polygon that is inscribed in any strictly convex curve, with its vertices in order along the curve, must be a convex polygon.^[20] A scaled and rotated copy of any rectangle or trapezoid can be inscribed in any given closed convex curve. When the curve is smooth, a scaled and rotated copy of any cyclic quadrilateral can be inscribed in it.^[21]^[22]

Notes

^ The assumption of smoothness is necessary when defining convex curves using tangent lines. There exist fractal curves, and even the graphs of continuous functions, that do not have any tangent lines, not even vertical or one-sided tangents.^[6] For these curves it is vacuously true that they lie on one side of each tangent line, but they are not convex.
^ For a slab, the region between two parallel lines, the boundary is its two defining lines.^[7]
^ The definition of convex curves as locally equivalent to graphs of convex functions requires strictness, because every polygonal chain looks locally like the graph of a piecewise linear convex function, even when the chain is not convex. However, other local definitions of convex curves, for instance as the parameterized simple curves with non-negative curvature, do not require strictness.
^ In characterizing smooth closed convex curves by the non-existence of three parallel tangents, it is necessary to specify that the curve be closed. There exist smooth but non-closed curves that do not have three parallel tangents but are not convex; the witch of Agnesi is an example.
^ In the characterization of convex smooth simple closed curves by their curvature, one must assume that the curve is simple, because some self-crossing curves such as the rose curves are not convex but have consistently-signed curvatures.^[16]

References

^ ^a ^b Banchoff, Thomas F.; Lovett, Stephen T. (2016), "Chapter 1: Plane curves: local properties", Differential Geometry of Curves and Surfaces (2nd ed.), CRC Press, pp. 1–46, ISBN 978-1-4822-4737-4
^ ^a ^b ^c ^d ^e Toponogov, Victor A. (2006), "1.5 Problems: convex plane curves", Differential Geometry of Curves and Surfaces: A Concise Guide, Birkhäuser, pp. 15–19, doi:10.1007/b137116, ISBN 978-0-8176-4402-4
^ Rademacher, Hans; Toeplitz, Otto (1994), The Enjoyment of Math, Princeton Science Library, Princeton University Press, Princeton, NJ, p. 164, ISBN 0-691-02351-4, MR 1300411
^ Epstein, Charles L. (2008), Introduction to the Mathematics of Medical Imaging (2nd ed.), Society for Industrial and Applied Mathematics, p. 17, ISBN 978-0-89871-779-2
^ ^a ^b ^c ^d Gray, Alfred; Abbena, Elsa; Salamon, Simon (2006), "6.4 Convex plane curves", Modern Differential Geometry of Curves and Surfaces with Mathematica (3rd ed.), Boca Raton: CRC Press, pp. 164–166, ISBN 978-1-58488-448-4; note that (per Definition 1.5, p. 5) this source assumes that the curves it describes are all piecewise smooth.
^ Ciesielski, Krzysztof Chris (2022), "Continuous maps admitting no tangent lines: a centennial of Besicovitch functions", The American Mathematical Monthly, 129 (7): 647–659, doi:10.1080/00029890.2022.2071562, MR 4457737
^ Preparata, Franco P.; Shamos, Michael Ian (1985), "2.2.2.1 The slab method", Computational Geometry: An Introduction, New York: Springer, pp. 45–48, doi:10.1007/978-1-4612-1098-6
^ Banchoff & Lovett (2016), p. 65.
^ ^a ^b ^c Polster, Burkard; Steinke, Günter (2001), "2.2.1 Convex curves, arcs, and ovals", Geometries on surfaces, Encyclopedia of Mathematics and its Applications, vol. 84, Cambridge University Press, pp. 31–34, doi:10.1017/CBO9780511549656, ISBN 0-521-66058-0, MR 1889925
^ Ricci, Fulvio; Travaglini, Giancarlo (2001), "Convex curves, Radon transforms and convolution operators defined by singular measures", Proceedings of the American Mathematical Society, 129 (6): 1739–1744, doi:10.1090/S0002-9939-00-05751-8, MR 1814105
^ Arnold, V. I. (1989), "Topological proof of the transcendence of the abelian integrals in Newton's Principia", Istoriko-Matematicheskie Issledovaniya (31): 7–17, ISSN 0136-0949, MR 0993175
^ Bordellès, Olivier (2012), "5.4.7 Counting integer points on smooth curves", Arithmetic Tales, Springer, p. 290, ISBN 9781447140962
^ Kakeya, Sōichi (1915), "On some properties of convex curves and surfaces.", Tohoku Mathematical Journal, 8: 218–221, JFM 45.1348.02
^ Martinez-Maure, Yves (2001), "A fractal projective hedgehog", Demonstratio Mathematica, 34 (1): 59–63, doi:10.1515/dema-2001-0108, MR 1823083
^ DeTruck, Dennis; Gluck, Herman; Pomerleano, Daniel; Vick, David Shea (2007), "The four vertex theorem and its converse" (PDF), Notices of the American Mathematical Society, 54 (2): 9268, arXiv:math/0609268
^ Cieślak, Waldemar; Zając, Józef (1986), "The rosettes", Mathematica Scandinavica, 58 (1): 114–118, doi:10.7146/math.scand.a-12133, JSTOR 24491607, MR 0845490
^ Chen, Bang-Yen (2000), "Riemannian submanifolds", Handbook of differential geometry, Vol. I, North-Holland, Amsterdam, pp. 187–418, doi:10.1016/S1874-5741(00)80006-0, MR 1736854; see in particular p. 360
^ Banchoff & Lovett (2016), p. 108.
^ Schwartzman, Steven (1994), The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English, MAA Spectrum, Mathematical Association of America, p. 156, ISBN 9780883855119
^ Milnor, J. W. (1950), "On the total curvature of knots", Annals of Mathematics, Second Series, 52: 248–257, doi:10.2307/1969467, JSTOR 1969467, MR 0037509; see discussion following Theorem 3.4 (Fenchel's theorem), p. 254
^ Akopyan, Arseniy; Avvakumov, Sergey (2018), "Any cyclic quadrilateral can be inscribed in any closed convex smooth curve", Forum of Mathematics, 6: Paper No. e7, 9, doi:10.1017/fms.2018.7, MR 3810027
^ Matschke, Benjamin (2021), "Quadrilaterals inscribed in convex curves", Transactions of the American Mathematical Society, 374 (8): 5719–5738, doi:10.1090/tran/8359, MR 4293786

[7] The assumption of smoothness is necessary when defining convex curves using tangent lines. There exist fractal curves, and even the graphs of continuous functions, that do not have any tangent lines, not even vertical or one-sided tangents.^[6] For these curves it is vacuously true that they lie on one side of each tangent line, but they are not convex.

[9] For a slab, the region between two parallel lines, the boundary is its two defining lines.^[7]

[13] The definition of convex curves as locally equivalent to graphs of convex functions requires strictness, because every polygonal chain looks locally like the graph of a piecewise linear convex function, even when the chain is not convex. However, other local definitions of convex curves, for instance as the parameterized simple curves with non-negative curvature, do not require strictness.

[18] In characterizing smooth closed convex curves by the non-existence of three parallel tangents, it is necessary to specify that the curve be closed. There exist smooth but non-closed curves that do not have three parallel tangents but are not convex; the witch of Agnesi is an example.

[21] In the characterization of convex smooth simple closed curves by their curvature, one must assume that the curve is simple, because some self-crossing curves such as the rose curves are not convex but have consistently-signed curvatures.^[16]

[banchoff-lovett-1] Banchoff, Thomas F.; Lovett, Stephen T. (2016), "Chapter 1: Plane curves: local properties", Differential Geometry of Curves and Surfaces (2nd ed.), CRC Press, pp. 1–46, ISBN 978-1-4822-4737-4

[toponogov-2] Toponogov, Victor A. (2006), "1.5 Problems: convex plane curves", Differential Geometry of Curves and Surfaces: A Concise Guide, Birkhäuser, pp. 15–19, doi:10.1007/b137116, ISBN 978-0-8176-4402-4

[rademacher-toeplitz-3] Rademacher, Hans; Toeplitz, Otto (1994), The Enjoyment of Math, Princeton Science Library, Princeton University Press, Princeton, NJ, p. 164, ISBN 0-691-02351-4, MR 1300411

[epstein-4] Epstein, Charles L. (2008), Introduction to the Mathematics of Medical Imaging (2nd ed.), Society for Industrial and Applied Mathematics, p. 17, ISBN 978-0-89871-779-2

[gray-5] Gray, Alfred; Abbena, Elsa; Salamon, Simon (2006), "6.4 Convex plane curves", Modern Differential Geometry of Curves and Surfaces with Mathematica (3rd ed.), Boca Raton: CRC Press, pp. 164–166, ISBN 978-1-58488-448-4; note that (per Definition 1.5, p. 5) this source assumes that the curves it describes are all piecewise smooth.

[ciesielski-6] Ciesielski, Krzysztof Chris (2022), "Continuous maps admitting no tangent lines: a centennial of Besicovitch functions", The American Mathematical Monthly, 129 (7): 647–659, doi:10.1080/00029890.2022.2071562, MR 4457737

[preparata-shamos-8] Preparata, Franco P.; Shamos, Michael Ian (1985), "2.2.2.1 The slab method", Computational Geometry: An Introduction, New York: Springer, pp. 45–48, doi:10.1007/978-1-4612-1098-6

[FOOTNOTEBanchoffLovett201665-10] Banchoff & Lovett (2016), p. 65.

[polster-steinke-11] Polster, Burkard; Steinke, Günter (2001), "2.2.1 Convex curves, arcs, and ovals", Geometries on surfaces, Encyclopedia of Mathematics and its Applications, vol. 84, Cambridge University Press, pp. 31–34, doi:10.1017/CBO9780511549656, ISBN 0-521-66058-0, MR 1889925

[ricci-travaglini-12] Ricci, Fulvio; Travaglini, Giancarlo (2001), "Convex curves, Radon transforms and convolution operators defined by singular measures", Proceedings of the American Mathematical Society, 129 (6): 1739–1744, doi:10.1090/S0002-9939-00-05751-8, MR 1814105

[arnold-14] Arnold, V. I. (1989), "Topological proof of the transcendence of the abelian integrals in Newton's Principia", Istoriko-Matematicheskie Issledovaniya (31): 7–17, ISSN 0136-0949, MR 0993175

[bordelles-15] Bordellès, Olivier (2012), "5.4.7 Counting integer points on smooth curves", Arithmetic Tales, Springer, p. 290, ISBN 9781447140962

[kakeya-16] Kakeya, Sōichi (1915), "On some properties of convex curves and surfaces.", Tohoku Mathematical Journal, 8: 218–221, JFM 45.1348.02

[martinez-maure-17] Martinez-Maure, Yves (2001), "A fractal projective hedgehog", Demonstratio Mathematica, 34 (1): 59–63, doi:10.1515/dema-2001-0108, MR 1823083

[dgpv-19] DeTruck, Dennis; Gluck, Herman; Pomerleano, Daniel; Vick, David Shea (2007), "The four vertex theorem and its converse" (PDF), Notices of the American Mathematical Society, 54 (2): 9268, arXiv:math/0609268

[cieslak-zajac-20] Cieślak, Waldemar; Zając, Józef (1986), "The rosettes", Mathematica Scandinavica, 58 (1): 114–118, doi:10.7146/math.scand.a-12133, JSTOR 24491607, MR 0845490

[chen-22] Chen, Bang-Yen (2000), "Riemannian submanifolds", Handbook of differential geometry, Vol. I, North-Holland, Amsterdam, pp. 187–418, doi:10.1016/S1874-5741(00)80006-0, MR 1736854; see in particular p. 360

[FOOTNOTEBanchoffLovett2016108-23] Banchoff & Lovett (2016), p. 108.

[schwartzman-24] Schwartzman, Steven (1994), The Words of Mathematics: An Etymological Dictionary of Mathematical Terms Used in English, MAA Spectrum, Mathematical Association of America, p. 156, ISBN 9780883855119

[milnor-25] Milnor, J. W. (1950), "On the total curvature of knots", Annals of Mathematics, Second Series, 52: 248–257, doi:10.2307/1969467, JSTOR 1969467, MR 0037509; see discussion following Theorem 3.4 (Fenchel's theorem), p. 254

[akopyan-avvakumov-26] Akopyan, Arseniy; Avvakumov, Sergey (2018), "Any cyclic quadrilateral can be inscribed in any closed convex smooth curve", Forum of Mathematics, 6: Paper No. e7, 9, doi:10.1017/fms.2018.7, MR 3810027

[matschke-27] Matschke, Benjamin (2021), "Quadrilaterals inscribed in convex curves", Transactions of the American Mathematical Society, 374 (8): 5719–5738, doi:10.1090/tran/8359, MR 4293786

[1]

[2]

[3]

[4]

[5]

[a]

[b]

[8]

[9]

[10]

[c]

[11]

[12]

[13]

[14]

[d]

[15]

[e]

[17]

[18]

[19]

[20]

[21]

[22]

[6]

[7]

[16]