Rectified 6-orthoplexes

6-orthoplex	Rectified 6-orthoplex	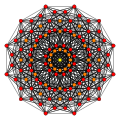Birectified 6-orthoplex
Birectified 6-cube	Rectified 6-cube	6-cube
Orthogonal projections in B6 Coxeter plane

In six-dimensional geometry, a rectified 6-orthoplex is a convex uniform 6-polytope, being a rectification of the regular 6-orthoplex.

There are unique 6 degrees of rectifications, the zeroth being the 6-orthoplex, and the 6th and last being the 6-cube. Vertices of the rectified 6-orthoplex are located at the edge-centers of the 6-orthoplex. Vertices of the birectified 6-orthoplex are located in the triangular face centers of the 6-orthoplex.

Rectified 6-orthoplex

Rectified hexacross
Type	uniform 6-polytope
Schläfli symbols	t1{34,4} or r{34,4} $\left\{{\begin{array}{l}3,3,3,4\\3\end{array}}\right\}$ r{3,3,3,31,1}
Coxeter-Dynkin diagrams	= =
5-faces	76 total: 64 rectified 5-simplex 12 5-orthoplex
4-faces	576 total: 192 rectified 5-cell 384 5-cell
Cells	1200 total: 240 octahedron 960 tetrahedron
Faces	1120 total: 160 and 960 triangles
Edges	480
Vertices	60
Vertex figure	16-cell prism
Petrie polygon	Dodecagon
Coxeter groups	B6, [3,3,3,3,4] D6, [33,1,1]
Properties	convex

The rectified 6-orthoplex is the vertex figure for the demihexeractic honeycomb.

or

Alternate names

• rectified hexacross
• rectified hexacontitetrapeton (acronym: rag) (Jonathan Bowers)

Construction

There are two Coxeter groups associated with the rectified hexacross, one with the C₆ or [4,3,3,3,3] Coxeter group, and a lower symmetry with two copies of pentacross facets, alternating, with the D₆ or [3^3,1,1] Coxeter group.

Cartesian coordinates

Cartesian coordinates for the vertices of a rectified hexacross, centered at the origin, edge length ${\sqrt {2}}\$ are all permutations of:

(±1,±1,0,0,0,0)

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph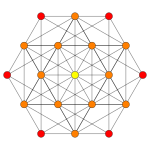
Dihedral symmetry	[6]	[4]

Root vectors

The 60 vertices represent the root vectors of the simple Lie group D₆. The vertices can be seen in 3 hyperplanes, with the 15 vertices rectified 5-simplices cells on opposite sides, and 30 vertices of an expanded 5-simplex passing through the center. When combined with the 12 vertices of the 6-orthoplex, these vertices represent the 72 root vectors of the B₆ and C₆ simple Lie groups.

The 60 roots of D₆ can be geometrically folded into H₃ (Icosahedral symmetry), as to , creating 2 copies of 30-vertex icosidodecahedra, with the Golden ratio between their radii:

Rectified 6-orthoplex		2 icosidodecahedra
3D (H3 projection)	A4/B5/D6 Coxeter plane	H2 Coxeter plane

Birectified 6-orthoplex

Birectified 6-orthoplex
Type	uniform 6-polytope
Schläfli symbols	t2{34,4} or 2r{34,4} $\left\{{\begin{array}{l}3,3,4\\3,3\end{array}}\right\}$ t2{3,3,3,31,1}
Coxeter-Dynkin diagrams	= =
5-faces	76
4-faces	636
Cells	2160
Faces	2880
Edges	1440
Vertices	160
Vertex figure	{3}×{3,4} duoprism
Petrie polygon	Dodecagon
Coxeter groups	B6, [3,3,3,3,4] D6, [33,1,1]
Properties	convex

The birectified 6-orthoplex can tessellation space in the trirectified 6-cubic honeycomb.

Alternate names

• birectified hexacross
• birectified hexacontitetrapeton (acronym: brag) (Jonathan Bowers)

Cartesian coordinates

Cartesian coordinates for the vertices of a rectified hexacross, centered at the origin, edge length ${\sqrt {2}}\$ are all permutations of:

(±1,±1,±1,0,0,0)

Images

orthographic projections

Coxeter plane	B6	B5	B4
Graph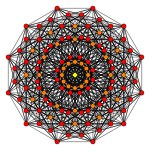
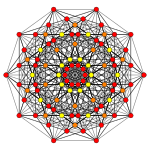
Dihedral symmetry	[12]	[10]	[8]
Coxeter plane	B3	B2
Graph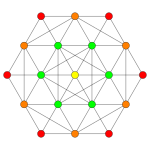
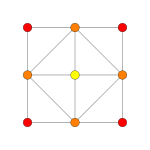
Dihedral symmetry	[6]	[4]
Coxeter plane	A5	A3
Graph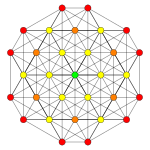
Dihedral symmetry	[6]	[4]

It can also be projected into 3D-dimensions as --> , a dodecahedron envelope.

Related polytopes

These polytopes are a part a family of 63 Uniform 6-polytopes generated from the B₆ Coxeter plane, including the regular 6-cube or 6-orthoplex.

References

• H.S.M. Coxeter:
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
    • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• Norman Johnson Uniform Polytopes, Manuscript (1991)
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
• Klitzing, Richard. "6D uniform polytopes (polypeta)". o3x3o3o3o4o - rag, o3o3x3o3o4o - brag

External links

• Polytopes of Various Dimensions
• Multi-dimensional Glossary